A hash tree or Merkle tree is a tree in which every non-leaf node is labelled with the hash of the labels or values (in case of leaves) of its child nodes. Hash trees are useful because they allow efficient and secure verification of the contents of large data structures.

Hash trees are used in the IPFS file system, BitTorrent protocol, Git, Bitcoin, Ethereum, and a number of NoSQL systems like Apache Cassandra and Riak.

They are used for many kinds of verification, especially of large chunks of data.

📬 Get updates straight to your inbox.

Subscribe to my newsletter so you don't miss new content.

Building a Merkle Tree

Say we’re building a file sharing system such as Bittorent, which involves sending blocks of data over the network. We want to verify the integrity and authenticity of our blocks. Blocks should arrive uncorrupted, and not altered by a malicious third party along the way.

How do we use the Merkle tree to efficiently do this?

The above diagram shows a binary Merkle tree. Each Node in a binary tree has two children.

defmodule MerkleTree.Node do
  @moduledoc """
    This module implements a tree node abstraction.
  """

  defstruct [:value, :children]

  @type t :: %MerkleTree.Node{
    value: String.t,
    children: [MerkleTree.Node.t],
  }
end

We have some blocks of data L1...L4.

A Merkle tree only contains hashes. To build our tree, we first create leaf nodes by hashing our data blocks with a hash_function such as SHA-2. This gives us 4 leaf nodes with values hash(L1)...hash(L4) respectively.

data_blocks = ["a", "b", "c", "d"]
hash_function = &MerkleTree.Crypto.sha256/1
leaves = Enum.map(data_blocks, fn(block) ->
  %MerkleTree.Node{
    value: hash_function.(block),
    children: [],
  }
end)

Next, we need to recursively build parent nodes whose values are equal to the hashes of its immediate children’s values. At each step, the number of nodes we have to work with will halve until only a single root node remains.

We calculate the hash of parent node by hashing the concatenation of its children’s values: hash(left_child.value <> right_child.value).

Below is an excerpt of the tree building code:

  @doc """
    Builds a new binary merkle tree.
  """
  @spec new(blocks, hash_function) :: root
  def build(blocks, hash_function) do
    leaves = Enum.map(blocks, fn(block) ->
      %MerkleTree.Node{
        value: hash_function.(block),
        children: [],
      }
    end)
    build_tree(leaves, hash_function)
  end

  defp build_tree([root], _), do: root # Base case
  defp build_tree(nodes, hash_function) do # Recursive case
    children_partitions = Enum.chunk(nodes, @number_of_children)
    parents = Enum.map(children_partitions, fn(partition) ->
      concatenated_values = partition
        |> Enum.map(&(&1.value))
        |> Enum.reduce("", fn(x, acc) -> acc <> x end)
      %MerkleTree.Node{
        value: hash_function.(concatenated_values),
        children: partition
      }
    end)
    build_tree(parents, hash_function)
  end

In the above code, we have a public build method that creates the initial leaves leaf nodes from our blocks, and passes it into the build_tree private function. The build_tree function recursively builds parent nodes until only a single root node is left, at which point root is returned.

Study the recursion in build_tree carefully.

Note that the implementation above is more general as it can accept trees with any arity, not just binary. Instead of doing left.value <> right.value, we use Enum.reduce to concatenate any number of children.

Verification

Looking at the above tree, we can see that only the root hash is necessary to verify that all the data blocks L1..L4 are valid. Consequently, the root hash can be sent through a trusted source.

We can then use this root hash to verify the integrity and authenticity of blocks. Once the root hash is available, the Merkle hash tree itself can be received from any non-trusted sources such as a peer in a P2P network. The received tree is then compared against the root hash. If the match fails, we move on to other peers and continue checking until we find a valid tree.

To verify if any individual data blocks are corrupted during transport or have been tampered with, we only need hashes on the log(n) path of nodes from a corrupted leaf up to the root will differ. In other words, we only need to ensure that the hashes of adjacent siblings/uncles are the same along the way up the tree. If any don’t match, either the leaf node is invalid or a sibling node along the log(n) path is invalid.

Application of Merkle proofs in Bitcoin

In Bitcoin, every transaction has a hash associated with it.

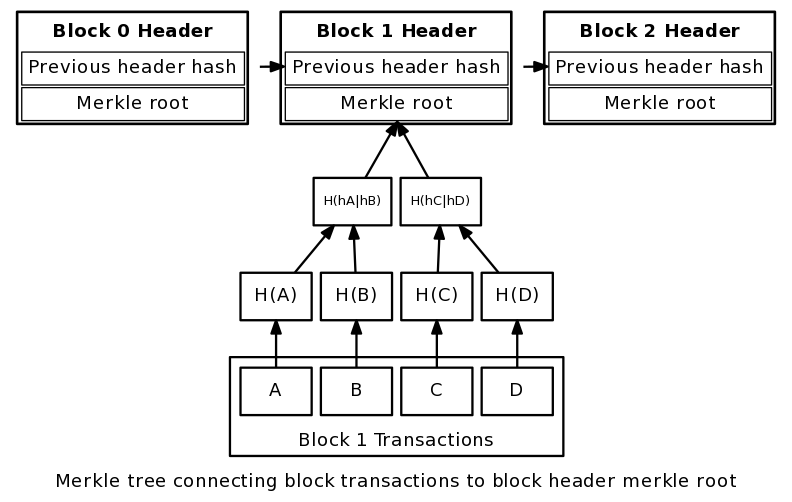
In a block, all of the transaction hashes in the block are themselves hashed (sometimes several times – the exact process is complex), and the result is the Merkle root. In other words, the Merkle root is the hash of all the hashes of all the transactions in the block. The Merkle root is included in the block header. With this scheme, it is possible to securely verify that a transaction has been accepted by the network (and get the number of confirmations) by downloading just the tiny block headers and Merkle tree – downloading the entire block chain is unnecessary.

Merkle trees allows for you to verify transactions as needed and not include the body of every transaction in the block header, while still providing a way to verify the entire blockchain (and therefore proof of work) on every transaction.

Application of Merkle proofs in IPFS

The InterPlanetary File System (IPFS) uses merkledag - a more generalized form of a Merkle tree. You can read more about it here.

Appendix: Elixir library

I’ve written a merkle_tree implementation in pure Elixir, making it easy for you to start using Merkle proofs in your applications.

Add merkle_tree to your list of dependencies in mix.exs:

def deps do
  [{:merkle_tree, "~> 1.1.0"}]
end

You can create trees like so:

iex> f = MerkleTree.new ['a', 'b', 'c', 'd']
%MerkleTree{blocks: ['a', 'b', 'c', 'd'], hash_function: &MerkleTree.Crypto.sha256/1,
      root: %MerkleTree.Node{children: [%MerkleTree.Node{children: [%MerkleTree.Node{children: [],
           value: "ca978112ca1bbdcafac231b39a23dc4da786eff8147c4e72b9807785afee48bb"},
          %MerkleTree.Node{children: [], value: "3e23e8160039594a33894f6564e1b1348bbd7a0088d42c4acb73eeaed59c009d"}],
         value: "62af5c3cb8da3e4f25061e829ebeea5c7513c54949115b1acc225930a90154da"},
        %MerkleTree.Node{children: [%MerkleTree.Node{children: [], value: "2e7d2c03a9507ae265ecf5b5356885a53393a2029d241394997265a1a25aefc6"},
          %MerkleTree.Node{children: [], value: "18ac3e7343f016890c510e93f935261169d9e3f565436429830faf0934f4f8e4"}],
         value: "d3a0f1c792ccf7f1708d5422696263e35755a86917ea76ef9242bd4a8cf4891a"}],
       value: "58c89d709329eb37285837b042ab6ff72c7c8f74de0446b091b6a0131c102cfd"}}

iex> f.root.value
58c89d709329eb37285837b042ab6ff72c7c8f74de0446b091b6a0131c102cfd

Appendix: Cryptographic hashing

The merkle_tree pure Elixir implementation uses SHA-2 as the default hash_function used and calls Erlang’s :crypto module for its hash implementations.

defmodule MerkleTree.Crypto do
  @moduledoc """
    This module defines some cryptographic hash functions used to hash block
    contents.
  """

  @type algorithm :: :md5 | :sha | :sha224 | :sha256 | :sha384 | :sha512

  @spec sha256(String.t) :: String.t
  def sha256(data) do
    hash(data, :sha256)
  end

  @spec hash(String.t, algorithm) :: String.t
  def hash(data, algorithm) do
    :crypto.hash(algorithm, data) |> Base.encode16(case: :lower)
  end
end

Conclusion

The Merkle hash tree is an incredible useful data structure used in a wide range of modern applications, such as peer-to-peer file sharing, cryptocurrencies, modern file systems, and more. They are used in many kinds of verification, especially of large chunks of data.